Sharp Blue: Maps of physics

On beginning a journey into a strange land (and modern physics is truly strange), it's useful to have an overview of the terrain to be crossed. This first part, then, will sketch maps of physics. How might we best draw these charts? One obvious way to carve the country of physics into provinces and states is to divide it along the borders that delineate the phenomena it models. In this view of physics, the fundamental divisions are disciplines such as nuclear physics, astrophysics, atomic physics, fluid mechanics, cosmology, solid state physics and so forth. Each of these fields is important for our understanding of the universe, they're each easily defined ("atomic physics is the study of atoms"), the problems they pose are easy to grasp (if less easy to solve), and their centrality is suggested by the groups of researchers studying them in university departments. On the other hand, they are each extremely complicated and don't interrelate in illuminating ways. However, what at first seems complex seems simpler if we think not in terms of the relationships between phenomena, but the relationships between theories.

Physics is not the search for truth. Instead, it is the search for useful theories. By a "useful" theory, I mean one that can be used to reproduce the results of past experiments and predict the outcomes of future ones. Physics proceeds by the invention, synthesis, testing and discarding of such theories. More exactly, what physicists deal with isn't so much theories in their pristine state, but paradigms, which are methods for using a theory to solve a particular problem. Much of the time in undergraduate physics courses is spent imparting the knowledge of such paradigms, which are then used as templates for the solving of other problems. A theory is good if it provides simple, general and accurate paradigms. In practice, the paradigms often precede the formulation of the theory as a logical, axiomatic structure - at first there is only a collection of ad hoc techniques, out of which the theory condenses by a series of insights and unifications. Paradigms are thus the anchors that pin the ghostly world of theory to the solid world of experiment.

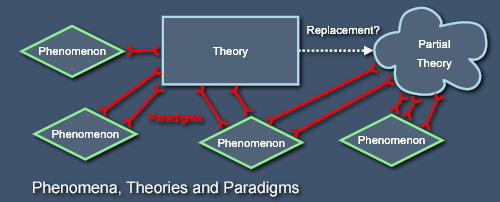
I don't believe that physics will ever yield an ultimate theory (to do so would be like an artist painting a perfect representation of her subject). However, even if I'm wrong and one day this quest for usefulness turns out to yield an ultimate truth - which is to say that we find a theory of everything - it will still coexist with other theories that are less comprehensive in their scope but also closer to our everyday world or less intractable in calculations. To understand physics deeply is thus (and always will be) to understand the concepts underlying our patchwork of theories and the relationships between them. In writing Light, the Universe, and Everything I hope to convey at least some understanding of these concepts and relationships, and some appreciation of the beauty, elegance and power of our best theories. I'll be concerned with the abstract world of these theories much more than with the world of experiments or the history of science (interesting though those undoubtedly are).

With this goal in mind, let's consider a look at the historical development of our most fundamental theories over the last century or so. Each of these theories is in a sense an entire world, for each is supposed to be universal in its scope. Each is a way that the real world could be, and yet none of them is the way the real world is - we know this because we have two theories that each explain various parts of the universe but which are seemingly incompatible. These two theories are quantum field theory, which forms the background to our theories of electromagnetism and the weak and strong nuclear forces, and general relativity, a theory of space, time and gravitation. Before considering the conceptual structures of these theories and their relationship to each other in more detail, let's summarise the recent history of physics in a diagram:

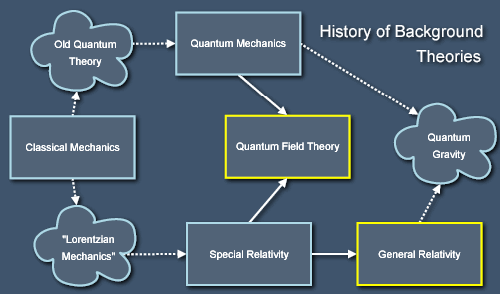
General relativity was invented by Einstein as a modification of his earlier theory of special relativity, which is the theory of the behaviour of space and time as seen by travellers in uniform relative motion (but which didn't include gravity). Special relativity in turn was developed from the earlier theory of classical mechanics, which is a theory originating in the work of Newton that works well for modelling the behaviour of our everyday world but which fails to match experimental data for fast-moving objects and, especially, light. Between the demise of classical mechanics as a fundamental theory and the rise of special relativity there was a period of confusion during which physicists tried to modify classical mechanics in increasingly desperate ways to make it fit the observed facts. For lack of a better name, I've called this theory "Lorentzian mechanics" because it was partly developed by Lorentz (and also by the likes of Fitzgerald, Lamour and Poincaré).

Classical mechanics also broke down in another way when physicists in the late 19th century began to study the behaviour of atoms. It was eventually superceded in that domain by a theory called quantum mechanics, in which measurements affect reality in irreducible ways, particles don't have definite positions and momenta at the same time, the universe is fundamentally probabilistic in its development, and many other strange things occur. From the fusion quantum mechanics and special relativity there then arose quantum field theory, which is a theory of things that are both small (like atoms) and fast (like light). Inspired by the successes of this theory in the field of particle physics, physicists have spent the last fifty years trying to merge not just special relativity and quantum mechanics but general relativity and quantum mechanics. This fusion would yield a theory of quantum gravity and probably much else besides. Indeed, it could potentially lead to a theory of everything, or at least a comprehensive theory of all known phenomena. In any case, this is getting ahead of ourselves.

The particular sequence of historical developments leading from classical mechanics to quantum field theory and general relativity isn't the clearest way to understand the structure of modern physics though. The problem is that two different sets of developments are entangled and confused in those theories. One development takes our ideas of space and time from the absolute space and time of Newton through the absolute spacetime of Minkowski to the curved manifold of general relativity. The other development replaces the deterministic, localised dynamics of classical Newtonian physics with the probabilistic, non-local dynamics of quantum theory. These various sets of ideas are actually more independent than they might seem at first glance, because they are always stirred together in various combinations to make full theories:

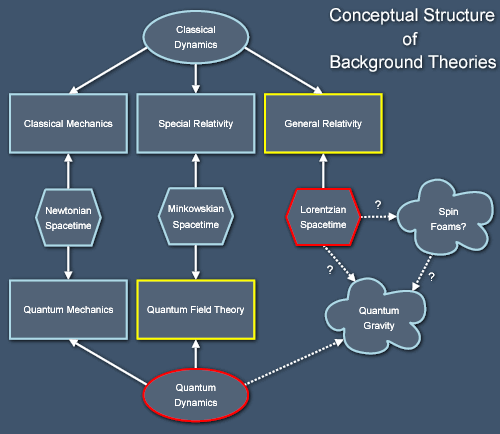
Each of the theories has its own flavour and the development in each strand (from classical mechanics to special relativity to general relativity and from quantum mechanics to quantum field theory) has resulted in surprising new phenomena that might not have been predicted from the spacetime and dynamical theories individually. Our two leading theories are each one step behind where we might hope to be, because general relativity uses an outdated theory of the nature of matter, and quantum field theory uses an outdated theory of the structure of space and time. As mentioned earlier, the next step now seems clear: to combine quantum theory with the framework of Lorentzian spacetime into a theory of quantum gravity.

This final (for now!) unification of our background theories has proven much harder than might at first have been expected, because the structures of spacetime and the laws governing matter aren't fully independent and interchangeable. The consensus amongst physicists seems to be that we may have to discard the smooth manifold of general relativity in favour of a more "quantum friendly" structure for space and time, perhaps one based on spin foams. Unfortunately, we don't really understand spin foams very well yet. There are even more radical schools of thought that we'll encounter later when I sketch the development of our ideas about forces. For now, though, the lower right region of the previous diagram will have to remain vague and undefined.

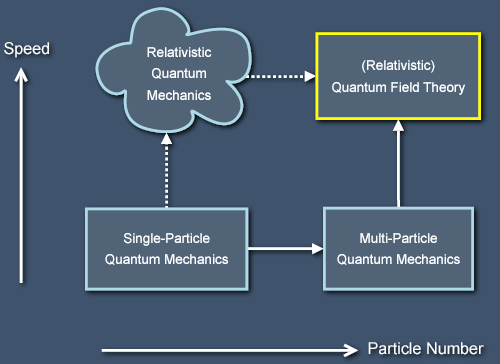
We can get a flavour for the kinds of difficulties involved in making a theory of quantum gravity by considering the difficulties involved in the earlier union of special-relativistic spacetime and quantum mechanics. Unlike quantum gravity, quantum field theory arises by taking very seriously all the postulates of both special relativity and quantum mechanics (the postulates of special relativity don't mention forces and suchlike at all, and nor do those of quantum mechanics specify a structure of space, although they do implicitly restrict the nature of time). Even so, the most obvious approach to making a (special-)relativistic theory of quantum mechanics runs into a host of problems. The path into this "quantum quagmire" leads from a simple idea: we know a way to make a quantum theory of a particle from a non-relativistic classical theory of a single particle, so we could try doing the same thing with a relativistic classical theory of a single particle. Unfortunately, the resulting theory is a mess that is full of difficulties with interpretation. The correct path leading from the quantum mechanics of a single particle to quantum field theory passes instead through the pleasant plains of multi-particle non-relativistic quantum mechanics:

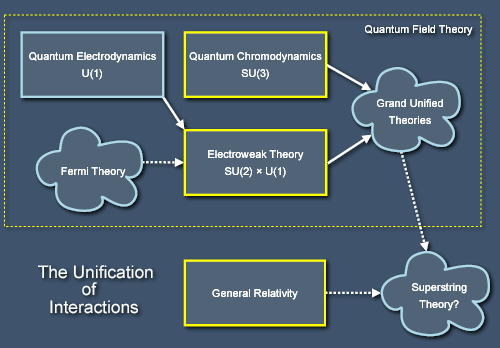
While we're examining quantum field theory, we can take a look at the relationships between our theories of the four forces of nature. Three of these are contained within the box "quantum field theory" on the previous diagrams. One of these forces, the weak nuclear force, considered on its own by way of Fermi's theory leads to a number of problems, and it's best to consider it as one aspect of the "electroweak" force, the other aspect of which is electromagnetism (itself a unification of the electric and magnetic forces that are familiar from our everyday world). If we just consider the electroweak and strong interactions then we're actually dealing with a subset of quantum field theory that deals with quantised gauge fields, which are theories based on a certain class of (somewhat abstract) geometric symmetries called gauge symmetries.

The success of the unification of the weak and electromagnetic theories has lead to some hopes that we might find a gauge symmetry that contains both the electroweak symmetry and the strong force's gauge symmetry, and this would lead us to a "Grand Unified Theory" that contains all the forces bar gravity. There are even hints that we might be able to fit gravity too into this framework, because its symmetry called "general covariance" is akin to the gauge theories of the other forces - they're all based around the idea called "coordinate independence". Even the step to a grand unified theory has proven problematic - and some think that we might have to take the leap to a theory of everything in one go. Maybe this theory will be superstring theory or M-theory, but maybe not. I'll have more to say about this in future chapters. So, once more we arrive at the frontiers of knowledge:

This article is just a freehand sketch of my first chapter, so I'll stop here. Of course, there's much more to be described: how the relationships between the gauge theories described above closely mirror the variation of strengths of the interactions with energy; how we can also change our degree of focus to take us from exact mechanics through statistical mechanics to thermodynamics; the treatment of some theories as approximations to others; the nature and limitations of the quantisation process; the relationship of physics to the underlying mathematics; and many other things. And I haven't even started to describe the inner workings of any of these theories. Those workings will have to wait for other sketches, or for Light, the Universe, and Everything itself.

Update (20/2/2004): Alan Forrester has posted a reply to this essay. It’s worth reading, even if I think he’s misunderstood me (as I explain in my response, “Science and Truth”).

Next in Series: “Science and Truth” >>